Polarization
Polarization (also polarisation) is a property applying to transverse waves that specifies the geometrical orientation of theoscillations.[1][2][3][4][5] In a transverse wave, the direction of the oscillation is transverse to the direction of motion of the wave, so the oscillations can have different directions perpendicular to the wave direction.[4] A simple example of a polarized transverse wave is vibrations traveling along a taut string(see image); for example, in a musical instrument like a guitar string. Depending on how the string is plucked, the vibrations can be in a vertical direction, horizontal direction, or at any angle perpendicular to the string. In contrast, in longitudinal waves, such as sound waves in a liquid or gas, the displacement of the particles in the oscillation is always in the direction of propagation, so these waves do not exhibit polarization. Transverse waves that exhibit polarization includeelectromagnetic waves such as light andradio waves, gravitational waves,[6] and transverse sound waves (shear waves) in solids. In some types of transverse waves, the wave displacement is limited to a single direction, so these also do not exhibit polarization; for example, in surface waves in liquids (gravity waves), the wave displacement of the particles is always in a vertical plane.
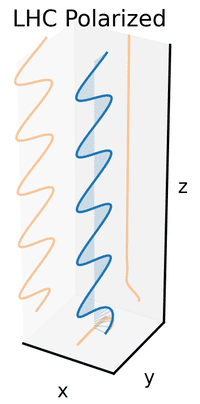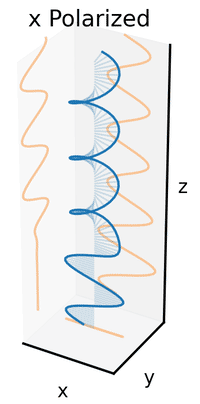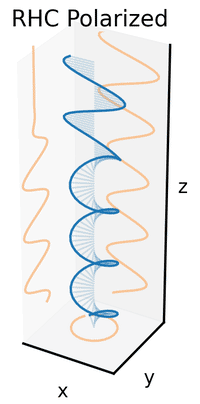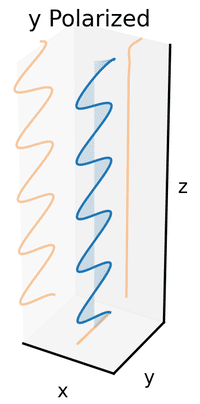
An electromagnetic wave such as light consists of a coupled oscillating electric fieldand magnetic field which are always perpendicular; by convention, the "polarization" of electromagnetic waves refers to the direction of the electric field. In linear polarization, the fields oscillate in a single direction. In circular or elliptical polarization, the fields rotate at a constant rate in a plane as the wave travels. The rotation can have two possible directions; if the fields rotate in aright hand sense with respect to the direction of wave travel, it is called right circular polarization, or, if the fields rotate in a left hand sense, it is called left circular polarization.
Light or other electromagnetic radiation from many sources, such as the sun, flames, andincandescent lamps, consists of short wave trains with an equal mixture of polarizations; this is called unpolarized light. Polarized light can be produced by passing unpolarized light through a polarizing filter, which allows waves of only one polarization to pass through. The most common optical materials (such as glass) are isotropic and do not affect the polarization of light passing through them; however, some materials—those that exhibitbirefringence, dichroism, or optical activity—can change the polarization of light. Some of these are used to make polarizing filters. Light is also partially polarized when it reflects from a surface.
According to quantum mechanics, electromagnetic waves can also be viewed as streams of particles called photons. When viewed in this way, the polarization of an electromagnetic wave is determined by a quantum mechanical property of photons called their spin. A photon has one of two possible spins: it can either spin in a right hand sense or a left hand sense about its direction of travel. Circularly polarized electromagnetic waves are composed of photons with only one type of spin, either right- or left-hand. Linearly polarized waves consist of equal numbers of right and left hand spinning photons, with their phase synchronized so they superpose to give oscillation in a plane.
Polarization is an important parameter in areas of science dealing with transverse waves, such as optics, seismology, radio, andmicrowaves. Especially impacted are technologies such as lasers, wireless and optical fiber telecommunications, and radar.
Introduction
Wave propagation and polarization
Most sources of light are classified as incoherent and unpolarized (or only "partially polarized") because they consist of a random mixture of waves having different spatial characteristics, frequencies (wavelengths), phases, and polarization states. However, for understanding electromagnetic waves and polarization in particular, it is easiest to just consider coherent plane waves; these are sinusoidal waves of one particular direction (or wavevector), frequency, phase, and polarization state. Characterizing an optical system in relation to a plane wave with those given parameters can then be used to predict its response to a more general case, since a wave with any specified spatial structure can be decomposed into a combination of plane waves (its so-called angular spectrum). And incoherent states can be modeledstochastically as a weighted combination of such uncorrelated waves with somedistribution of frequencies (its spectrum), phases, and polarizations.
Transverse electromagnetic waves
Electromagnetic waves (such as light), traveling in free space or anotherhomogeneous isotropic non-attenuatingmedium, are properly described as transverse waves, meaning that a plane wave's electric field vector E and magnetic field H are in directions perpendicular to (or "transverse" to) the direction of wave propagation; E and H are also perpendicular to each other. Considering a monochromatic plane wave of optical frequency f (light of vacuum wavelength λ has a frequency of f = c/λ where c is the speed of light), let us take the direction of propagation as the z axis. Being a transverse wave the Eand H fields must then contain components only in the x and y directions whereasEz=Hz=0. Using complex (or phasor) notation, we understand the instantaneous physical electric and magnetic fields to be given by thereal parts of the complex quantities occurring in the following equations. As a function of time t and spatial position z (since for a plane wave in the +z direction the fields have no dependence on x or y) these complex fields can be written as:
and
where λ/n is the wavelength in the medium(whose refractive index is n) and T = 1/f is the period of the wave. Here ex, ey, hx, and hy are complex numbers. In the second more compact form, as these equations are customarily expressed, these factors are described using the wavenumber  and angular frequency (or "radian frequency")
and angular frequency (or "radian frequency")  . In a more general formulation with propagation notrestricted to the +z direction, then the spatial dependence kz is replaced by
. In a more general formulation with propagation notrestricted to the +z direction, then the spatial dependence kz is replaced by  where
where  is called the wave vector, the magnitude of which is the wavenumber.
is called the wave vector, the magnitude of which is the wavenumber.
 and angular frequency (or "radian frequency")
and angular frequency (or "radian frequency")  . In a more general formulation with propagation notrestricted to the +z direction, then the spatial dependence kz is replaced by
. In a more general formulation with propagation notrestricted to the +z direction, then the spatial dependence kz is replaced by  where
where  is called the wave vector, the magnitude of which is the wavenumber.
is called the wave vector, the magnitude of which is the wavenumber.
Thus the leading vectors e and h each contain up to two nonzero (complex) components describing the amplitude and phase of the wave's x and y polarization components (again, there can be no z polarization component for a transverse wave in the +zdirection). For a given medium with acharacteristic impedance  , h is related to eby:
, h is related to eby:
 , h is related to eby:
, h is related to eby:
and
.
In a dielectric, η is real and has the value η0/n, where n is the refractive index and η0 is the impedance of free space. The impedance will be complex in a conducting medium.[clarification needed] Note that given that relationship, the dot product of E and H must be zero:[dubious ]
indicating that these vectors are orthogonal(at right angles to each other), as expected.
So knowing the propagation direction (+z in this case) and η, one can just as well specify the wave in terms of just ex and ey describing the electric field. The vector containing ex andey (but without the z component which is necessarily zero for a transverse wave) is known as a Jones vector. In addition to specifying the polarization state of the wave, a general Jones vector also specifies the overall magnitude and phase of that wave. Specifically, the intensity of the light wave is proportional to the sum of the squared magnitudes of the two electric field components:
however the wave's state of polarization is only dependent on the (complex) ratio of ey toex. So let us just consider waves whose |ex|2 + |ey|2 = 1; this happens to correspond to an intensity of about .00133 watts per square meter in free space (where 
 ). And since the absolute phase of a wave is unimportant in discussing its polarization state, let us stipulate that the phase of ex is zero, in other words ex is a real number whileey may be complex. Under these restrictions,ex and ey can be represented as follows:
). And since the absolute phase of a wave is unimportant in discussing its polarization state, let us stipulate that the phase of ex is zero, in other words ex is a real number whileey may be complex. Under these restrictions,ex and ey can be represented as follows:

 ). And since the absolute phase of a wave is unimportant in discussing its polarization state, let us stipulate that the phase of ex is zero, in other words ex is a real number whileey may be complex. Under these restrictions,ex and ey can be represented as follows:
). And since the absolute phase of a wave is unimportant in discussing its polarization state, let us stipulate that the phase of ex is zero, in other words ex is a real number whileey may be complex. Under these restrictions,ex and ey can be represented as follows:
where the polarization state is now fully parameterized by the value of Q (such that −1 < Q < 1) and the relative phase  . By convention when one speaks of a wave's "polarization," if not otherwise specified, reference is being made to the polarization of the electric field. The polarization of the magnetic field always follows that of the electric field but with a 90 degree rotation, as detailed above.
. By convention when one speaks of a wave's "polarization," if not otherwise specified, reference is being made to the polarization of the electric field. The polarization of the magnetic field always follows that of the electric field but with a 90 degree rotation, as detailed above.
 . By convention when one speaks of a wave's "polarization," if not otherwise specified, reference is being made to the polarization of the electric field. The polarization of the magnetic field always follows that of the electric field but with a 90 degree rotation, as detailed above.
. By convention when one speaks of a wave's "polarization," if not otherwise specified, reference is being made to the polarization of the electric field. The polarization of the magnetic field always follows that of the electric field but with a 90 degree rotation, as detailed above.Non-transverse waves
In addition to transverse waves, there are many wave motions where the oscillation is not limited to directions perpendicular to the direction of propagation. These cases are far beyond the scope of the current article which concentrates on transverse waves (such as most electromagnetic waves in bulk media), however one should be aware of cases where the polarization of a coherent wave cannot be described simply using a Jones vector, as we have just done.
Just considering electromagnetic waves, we note that the preceding discussion strictly applies to plane waves in a homogeneous isotropic non-attenuating medium, whereas in an anisotropic medium (such as birefringent crystals as discussed below) the electric or magnetic field may have longitudinal as well as transverse components. In those cases theelectric displacement D and magnetic flux density B[clarification needed] still obey the above geometry but due to anisotropy in the electric susceptibility (or in the magnetic permeability), now given by a tensor, the direction of E (or H) may differ from that of D(or B). Even in isotropic media, so-calledinhomogeneous waves can be launched into a medium whose refractive index has a significant imaginary part (or "extinction coefficient") such as metals;[clarification needed]these fields are also not strictly transverse.[7]:179–184[8]:51–52 Surface waves or waves propagating in a waveguide (such as an optical fiber) are generally not transverse waves, but might be described as an electric or magnetic transverse mode, or a hybrid mode.
Even in free space, longitudinal field components can be generated in focal regions, where the plane wave approximation breaks down. An extreme example is radiallyor tangentially polarized light, at the focus of which the electric or magnetic field respectively is entirely longitudinal (along the direction of propagation).[9]
For longitudinal waves such as sound wavesin fluids, the direction of oscillation is by definition along the direction of travel, so the issue of polarization is not normally even mentioned. On the other hand, sound waves in a bulk solid can be transverse as well as longitudinal, for a total of three polarization components. In this case, the transverse polarization is associated with the direction of the shear stress and displacement in directions perpendicular to the propagation direction, while the longitudinal polarization describes compression of the solid and vibration along the direction of propagation. The differential propagation of transverse and longitudinal polarizations is important inseismology.
Polarization state
Polarization is best understood by initially considering only pure polarization states, and only a coherent sinusoidal wave at some optical frequency. The vector in the adjacent diagram might describe the oscillation of the electric field emitted by a single-mode laser (whose oscillation frequency would be typically 1015 times faster). The field oscillates in the x-y plane, along the page, with the wave propagating in the z direction, perpendicular to the page. The first two diagrams below trace the electric field vector over a complete cycle for linear polarization at two different orientations; these are each considered a distinct state of polarization(SOP). Note that the linear polarization at 45° can also be viewed as the addition of a horizontally linearly polarized wave (as in the leftmost figure) and a vertically polarized wave of the same amplitude in the same phase.
Now if one were to introduce a phase shift in between those horizontal and vertical polarization components, one would generally obtain elliptical polarization[10] as is shown in the third figure. When the phase shift is exactly ±90°, then circular polarization is produced (fourth and fifth figures). Thus is circular polarization created in practice, starting with linearly polarized light and employing a quarter-wave plate to introduce such a phase shift. The result of two such phase-shifted components in causing a rotating electric field vector is depicted in the animation on the right. Note that circular or elliptical polarization can involve either a clockwise or counterclockwise rotation of the field. These correspond to distinct polarization states, such as the two circular polarizations shown above.
Of course the orientation of the x and y axes used in this description is arbitrary. The choice of such a coordinate system and viewing the polarization ellipse in terms of thex and y polarization components, corresponds to the definition of the Jones vector (below) in terms of those basis polarizations. One would typically choose axes to suit a particular problem such as x being in the plane of incidence. Since there are separate reflection coefficients for the linear polarizations in and orthogonal to the plane of incidence (p and spolarizations, see below), that choice greatly simplifies the calculation of a wave's reflection from a surface.
Moreover, one can use as basis functions anypair of orthogonal polarization states, not just linear polarizations. For instance, choosing right and left circular polarizations as basis functions simplifies the solution of problems involving circular birefringence (optical activity) or circular dichroism.
Polarization ellipse
Consider a purely polarized monochromatic wave. If one were to plot the electric field vector over one cycle of oscillation, an ellipse would generally be obtained, as is shown in the figure, corresponding to a particular state of elliptical polarization. Note that linear polarization and circular polarization can be seen as special cases of elliptical polarization.
A polarization state can then be described in relation to the geometrical parameters of the ellipse, and its "handedness", that is, whether the rotation around the ellipse is clockwise or counter clockwise. One parameterization of the elliptical figure specifies the orientation angle ψ, defined as the angle between the major axis of the ellipse and the x-axis[11]along with the ellipticity ε=a/b, the ratio of the ellipse's major to minor axis.[12][13][14][15] (also known as the axial ratio). The ellipticity parameter is an alternative parameterization of an ellipse's eccentricity  , or the ellipticity angle, χ = arctan b/a= arctan 1/ε as is shown in the figure.[11] The angle χ is also significant in that the latitude (angle from the equator) of the polarization state as represented on the Poincaré sphere (see below) is equal to ±2χ. The special cases of linear and circular polarization correspond to an ellipticity ε of infinity and unity (or χ of zero and 45°) respectively.
, or the ellipticity angle, χ = arctan b/a= arctan 1/ε as is shown in the figure.[11] The angle χ is also significant in that the latitude (angle from the equator) of the polarization state as represented on the Poincaré sphere (see below) is equal to ±2χ. The special cases of linear and circular polarization correspond to an ellipticity ε of infinity and unity (or χ of zero and 45°) respectively.
 , or the ellipticity angle, χ = arctan b/a= arctan 1/ε as is shown in the figure.[11] The angle χ is also significant in that the latitude (angle from the equator) of the polarization state as represented on the Poincaré sphere (see below) is equal to ±2χ. The special cases of linear and circular polarization correspond to an ellipticity ε of infinity and unity (or χ of zero and 45°) respectively.
, or the ellipticity angle, χ = arctan b/a= arctan 1/ε as is shown in the figure.[11] The angle χ is also significant in that the latitude (angle from the equator) of the polarization state as represented on the Poincaré sphere (see below) is equal to ±2χ. The special cases of linear and circular polarization correspond to an ellipticity ε of infinity and unity (or χ of zero and 45°) respectively.Jones vector
Full information on a completely polarized state is also provided by the amplitude and phase of oscillations in two components of the electric field vector in the plane of polarization. This representation was used above to show how different states of polarization are possible. The amplitude and phase information can be conveniently represented as a two-dimensional complexvector (the Jones vector):
Here  and
and  denote the amplitude of the wave in the two components of the electric field vector, while
denote the amplitude of the wave in the two components of the electric field vector, while  and
and  represent the phases. The product of a Jones vector with a complex number of unit modulus gives a different Jones vector representing the same ellipse, and thus the same state of polarization. The physical electric field, as the real part of the Jones vector, would be altered but the polarization state itself is independent of absolute phase. The basis vectors used to represent the Jones vector need not represent linear polarization states (i.e. be real). In general any two orthogonal states can be used, where an orthogonal vector pair is formally defined as one having a zero inner product. A common choice is left and right circular polarizations, for example to model the different propagation of waves in two such components in circularly birefringent media (see below) or signal paths of coherent detectors sensitive to circular polarization.
represent the phases. The product of a Jones vector with a complex number of unit modulus gives a different Jones vector representing the same ellipse, and thus the same state of polarization. The physical electric field, as the real part of the Jones vector, would be altered but the polarization state itself is independent of absolute phase. The basis vectors used to represent the Jones vector need not represent linear polarization states (i.e. be real). In general any two orthogonal states can be used, where an orthogonal vector pair is formally defined as one having a zero inner product. A common choice is left and right circular polarizations, for example to model the different propagation of waves in two such components in circularly birefringent media (see below) or signal paths of coherent detectors sensitive to circular polarization.
 and
and  denote the amplitude of the wave in the two components of the electric field vector, while
denote the amplitude of the wave in the two components of the electric field vector, while  and
and  represent the phases. The product of a Jones vector with a complex number of unit modulus gives a different Jones vector representing the same ellipse, and thus the same state of polarization. The physical electric field, as the real part of the Jones vector, would be altered but the polarization state itself is independent of absolute phase. The basis vectors used to represent the Jones vector need not represent linear polarization states (i.e. be real). In general any two orthogonal states can be used, where an orthogonal vector pair is formally defined as one having a zero inner product. A common choice is left and right circular polarizations, for example to model the different propagation of waves in two such components in circularly birefringent media (see below) or signal paths of coherent detectors sensitive to circular polarization.
represent the phases. The product of a Jones vector with a complex number of unit modulus gives a different Jones vector representing the same ellipse, and thus the same state of polarization. The physical electric field, as the real part of the Jones vector, would be altered but the polarization state itself is independent of absolute phase. The basis vectors used to represent the Jones vector need not represent linear polarization states (i.e. be real). In general any two orthogonal states can be used, where an orthogonal vector pair is formally defined as one having a zero inner product. A common choice is left and right circular polarizations, for example to model the different propagation of waves in two such components in circularly birefringent media (see below) or signal paths of coherent detectors sensitive to circular polarization.Coordinate frame
Regardless of whether polarization state is represented using geometric parameters or Jones vectors, implicit in the parameterization is the orientation of the coordinate frame. This permits a degree of freedom, namely rotation about the propagation direction. When considering light that is propagating parallel to the surface of the Earth, the terms "horizontal" and "vertical" polarization are often used, with the former being associated with the first component of the Jones vector, or zero azimuth angle. On the other hand, inastronomy the equatorial coordinate systemis generally used instead, with the zero azimuth (or position angle, as it is more commonly called in astronomy to avoid confusion with the horizontal coordinate system) corresponding to due north.
s and p designations
Electromagnetic vectors for  ,
,  and
and  with
with  along with 3 planar projections and a deformation surface of total electric field. The light is always s-polarized in the xy plane.
along with 3 planar projections and a deformation surface of total electric field. The light is always s-polarized in the xy plane.  is the polar angle of
is the polar angle of  and
and  is the azimuthal angle of
is the azimuthal angle of  .
.
 ,
,  and
and  with
with  along with 3 planar projections and a deformation surface of total electric field. The light is always s-polarized in the xy plane.
along with 3 planar projections and a deformation surface of total electric field. The light is always s-polarized in the xy plane.  is the polar angle of
is the polar angle of  and
and  is the azimuthal angle of
is the azimuthal angle of  .
.
Another coordinate system frequently used relates to the plane of incidence. This is the plane made by the incoming propagation direction and the vector perpendicular to the plane of an interface, in other words, the plane in which the ray travels before and after reflection or refraction. The component of the electric field parallel to this plane is termed p-like (parallel) and the component perpendicular to this plane is termed s-like(from senkrecht, German for perpendicular). Polarized light with its electric field along the plane of incidence is thus denoted p-polarized, while light whose electric field is normal to the plane of incidence is called s-polarized. Ppolarization is commonly referred to astransverse-magnetic (TM), and has also been termed pi-polarized or tangential plane polarized. S polarization is also calledtransverse-electric (TE), as well as sigma-polarized or sagittal plane polarized.
Unpolarized and partially polarized light
Definition
Natural light, and most other common sources of visible light, are incoherent: radiation is produced independently by a large number of atoms or molecules whose emissions are uncorrelated and generally of random polarizations. In this case the light is said to be unpolarized. This term is somewhat inexact, since at any instant of time at one location there is a definite direction to the electric and magnetic fields, however it implies that the polarization changes so quickly in time that it will not be measured or relevant to the outcome of an experiment. A so-called depolarizer acts on a polarized beam to create one which is actually fullypolarized at every point, but in which the polarization varies so rapidly across the beam that it may be ignored in the intended applications.
Unpolarized light can be described as a mixture of two independent oppositely polarized streams, each with half the intensity.[16][17] Light is said to be partially polarized when there is more power in one of these streams than the other. At any particular wavelength, partially polarized light can be statistically described as the superposition of a completely unpolarized component and a completely polarized one.[18]:330 One may then describe the light in terms of the degree of polarization and the parameters of the polarized component. That polarized component can be described in terms of a Jones vector or polarization ellipse, as is detailed above. However, in order to also describe the degree of polarization, one normally employs Stokes parameters (see below) to specify a state of partial polarization.[18]:351,374–375
Motivation
The transmission of plane waves through a homogeneous medium are fully described in terms of Jones vectors and 2×2 Jones matrices. However, in practice there are cases in which all of the light cannot be viewed in such a simple manner due to spatial inhomogeneities or the presence of mutually incoherent waves. So-called depolarization, for instance, cannot be described using Jones matrices. For these cases it is usual instead to use a 4×4 matrix that acts upon the Stokes 4-vector. Such matrices were first used by Paul Soleillet in 1929, although they have come to be known as Mueller matrices. While every Jones matrix has a Mueller matrix, the reverse is not true. Mueller matrices are then used to describe the observed polarization effects of the scattering of waves from complex surfaces or ensembles of particles, as shall now be presented.[18]:377–379
Coherency matrix
The Jones vector perfectly describes the state of polarization and phase of a single monochromatic wave, representing a pure state of polarization as described above. However any mixture of waves of different polarizations (or even of different frequencies) do not correspond to a Jones vector. In so-called partially polarized radiation the fields are stochastic, and the variations and correlations between components of the electric field can only be described statistically. One such representation is the coherencymatrix:[19]:137–142
where angular brackets denote averaging over many wave cycles. Several variants of the coherency matrix have been proposed: theWiener coherency matrix and the spectral coherency matrix of Richard Barakat measure the coherence of a spectral decomposition of the signal, while the Wolf coherency matrix averages over all time/frequencies.
The coherency matrix contains all second order statistical information about the polarization. This matrix can be decomposed into the sum of two idempotent matrices, corresponding to the eigenvectors of the coherency matrix, each representing a polarization state that is orthogonal to the other. An alternative decomposition is into completely polarized (zero determinant) and unpolarized (scaled identity matrix) components. In either case, the operation of summing the components corresponds to the incoherent superposition of waves from the two components. The latter case gives rise to the concept of the "degree of polarization"; i.e., the fraction of the total intensity contributed by the completely polarized component.
Stokes parameters
The coherency matrix is not easy to visualize, and it is therefore common to describe incoherent or partially polarized radiation in terms of its total intensity (I), (fractional) degree of polarization (p), and the shape parameters of the polarization ellipse. An alternative and mathematically convenient description is given by the Stokes parameters, introduced by George Gabriel Stokes in 1852. The relationship of the Stokes parameters to intensity and polarization ellipse parameters is shown in the equations and figure below.
Here Ip, 2ψ and 2χ are the spherical coordinates of the polarization state in the three-dimensional space of the last three Stokes parameters. Note the factors of two before ψ and χ corresponding respectively to the facts that any polarization ellipse is indistinguishable from one rotated by 180°, or one with the semi-axis lengths swapped accompanied by a 90° rotation. The Stokes parameters are sometimes denoted I, Q, U andV.
Poincaré sphere
Neglecting the first Stokes parameter S0 (or I), the three other Stokes parameters can be plotted directly in three-dimensional Cartesian coordinates. For a given power in the polarized component given by
the set of all polarization states are then mapped to points on the surface of the so-called Poincaré sphere (but of radius P), as shown in the accompanying diagram.
Often the total beam power is not of interest, in which case a normalized Stokes vector is used by dividing the Stokes vector by the total intensity S0:
The normalized Stokes vector then has unity power ( ) and the three significant Stokes parameters plotted in three dimensions will lie on the unity-radius Poincaré sphere for pure polarization states (where ). Partially polarized states will lie inside the Poincaré sphere at a distance of from the origin. When the non-polarized component is not of interest, the Stokes vector can be further normalized to obtain
When plotted, that point will lie on the surface of the unity-radius Poincaré sphere and indicate the state of polarization of the polarized component.
Any two antipodal points on the Poincaré sphere refer to orthogonal polarization states. The overlap between any two polarization states is dependent solely on the distance between their locations along the sphere. This property, which can only be true when pure polarization states are mapped onto a sphere, is the motivation for the invention of the Poincaré sphere and the use of Stokes parameters, which are thus plotted on (or beneath) it.
Implications for reflection and propagation
Polarization in wave propagation
In a vacuum, the components of the electric field propagate at the speed of light, so that the phase of the wave varies in space and time while the polarization state does not. That is, the electric field vector e of a plane wave in the +z direction follows:
where k is the wavenumber. As noted above, the instantaneous electric field is the real part of the product of the Jones vector times the phase factor  . When an electromagnetic wave interacts with matter, its propagation is altered according to the material's (complex)index of refraction. When the real or imaginary part of that refractive index is dependent on the polarization state of a wave, properties known as birefringence and polarizationdichroism (or diattenuation) respectively, then the polarization state of a wave will generally be altered.
. When an electromagnetic wave interacts with matter, its propagation is altered according to the material's (complex)index of refraction. When the real or imaginary part of that refractive index is dependent on the polarization state of a wave, properties known as birefringence and polarizationdichroism (or diattenuation) respectively, then the polarization state of a wave will generally be altered.
 . When an electromagnetic wave interacts with matter, its propagation is altered according to the material's (complex)index of refraction. When the real or imaginary part of that refractive index is dependent on the polarization state of a wave, properties known as birefringence and polarizationdichroism (or diattenuation) respectively, then the polarization state of a wave will generally be altered.
. When an electromagnetic wave interacts with matter, its propagation is altered according to the material's (complex)index of refraction. When the real or imaginary part of that refractive index is dependent on the polarization state of a wave, properties known as birefringence and polarizationdichroism (or diattenuation) respectively, then the polarization state of a wave will generally be altered.
In such media, an electromagnetic wave with any given state of polarization may be decomposed into two orthogonally polarized components that encounter differentpropagation constants. The effect of propagation over a given path on those two components is most easily characterized in the form of a complex 2×2 transformationmatrix J known as a Jones matrix:
The Jones matrix due to passage through a transparent material is dependent on the propagation distance as well as the birefringence. The birefringence (as well as the average refractive index) will generally bedispersive, that is, it will vary as a function of optical frequency (wavelength). In the case of non-birefringent materials, however, the 2×2 Jones matrix is the identity matrix (multiplied by a scalar phase factor and attenuation factor), implying no change in polarization during propagation.
For propagation effects in two orthogonal modes, the Jones matrix can be written as
where g1 and g2 are complex numbers describing the phase delay and possibly the amplitude attenuation due to propagation in each of the two polarization eigenmodes. T is a unitary matrix representing a change of basis from these propagation modes to the linear system used for the Jones vectors; in the case of linear birefringence or diattenuation the modes are themselves linear polarization states so T and T−1 can be omitted if the coordinate axes have been chosen appropriately.
Birefringence
In media termed birefringent, in which the amplitudes are unchanged but a differential phase delay occurs, the Jones matrix is aunitary matrix: |g1| = |g2| = 1. Media termed diattenuating (or dichroic in the sense of polarization), in which only the amplitudes of the two polarizations are affected differentially, may be described using aHermitian matrix (generally multiplied by a common phase factor). In fact, since anymatrix may be written as the product of unitary and positive Hermitian matrices, light propagation through any sequence of polarization-dependent optical components can be written as the product of these two basic types of transformations.
Color pattern of a plastic box showingstress-induced birefringence when placed in between two crossed polarizers.
In birefringent media there is no attenuation, but two modes accrue a differential phase delay. Well known manifestations of linear birefringence (that is, in which the basis polarizations are orthogonal linear polarizations) appear in optical wave plates/retarders and many crystals. If linearly polarized light passes through a birefringent material, its state of polarization will generally change, unless its polarization direction is identical to one of those basis polarizations. Since the phase shift, and thus the change in polarization state, is usually wavelength-dependent, such objects viewed under white light in between two polarizers may give rise to colorful effects, as seen in the accompanying photograph.
Circular birefringence is also termed optical activity, especially in chiral fluids, or Faraday rotation, when due to the presence of a magnetic field along the direction of propagation. When linearly polarized light is passed through such an object, it will exit still linearly polarized, but with the axis of polarization rotated. A combination of linear and circular birefringence will have as basis polarizations two orthogonal elliptical polarizations; however, the term "elliptical birefringence" is rarely used.
One can visualize the case of linear birefringence (with two orthogonal linear propagation modes) with an incoming wave linearly polarized at a 45° angle to those modes. As a differential phase starts to accrue, the polarization becomes elliptical, eventually changing to purely circular polarization (90° phase difference), then to elliptical and eventually linear polarization (180° phase) perpendicular to the original polarization, then through circular again (270° phase), then elliptical with the original azimuth angle, and finally back to the original linearly polarized state (360° phase) where the cycle begins anew. In general the situation is more complicated and can be characterized as a rotation in the Poincaré sphere about the axis defined by the propagation modes. Examples for linear (blue), circular (red), and elliptical (yellow) birefringence are shown in the figure on the left. The total intensity and degree of polarization are unaffected. If the path length in the birefringent medium is sufficient, the two polarization components of a collimated beam (or ray) can exit the material with a positional offset, even though their final propagation directions will be the same (assuming the entrance face and exit face are parallel). This is commonly viewed using calcite crystals, which present the viewer with two slightly offset images, in opposite polarizations, of an object behind the crystal. It was this effect that provided the first discovery of polarization, by Erasmus Bartholinus in 1669.
Dichroism
Media in which transmission of one polarization mode is preferentially reduced are called dichroic or diattenuating. Like birefringence, diattenuation can be with respect to linear polarization modes (in a crystal) or circular polarization modes (usually in a liquid).
Devices that block nearly all of the radiation in one mode are known as polarizing filters or simply "polarizers". This corresponds to g2=0 in the above representation of the Jones matrix. The output of an ideal polarizer is a specific polarization state (usually linear polarization) with an amplitude equal to the input wave's original amplitude in that polarization mode. Power in the other polarization mode is eliminated. Thus if unpolarized light is passed through an ideal polarizer (where g1=1 and g2=0) exactly half of its initial power is retained. Practical polarizers, especially inexpensive sheet polarizers, have additional loss so that g1 < 1. However, in many instances the more relevant figure of merit is the polarizer's degree of polarization or extinction ratio, which involve a comparison of g1 to g2. Since Jones vectors refer to waves' amplitudes (rather thanintensity), when illuminated by unpolarized light the remaining power in the unwanted polarization will be (g2/g1)2 of the power in the intended polarization.
Specular reflection
In addition to birefringence and dichroism in extended media, polarization effects describable using Jones matrices can also occur at (reflective) interface between two materials of different refractive index. These effects are treated by the Fresnel equations. Part of the wave is transmitted and part is reflected; for a given material those proportions (and also the phase of reflection) are dependent on the angle of incidence and are different for the s and p polarizations. Therefore, the polarization state of reflected light (even if initially unpolarized) is generally changed.
Any light striking a surface at a special angle of incidence known as Brewster's angle, where the reflection coefficient for ppolarization is zero, will be reflected with only the s-polarization remaining. This principle is employed in the so-called "pile of plates polarizer" (see figure) in which part of the spolarization is removed by reflection at each Brewster angle surface, leaving only the ppolarization after transmission through many such surfaces. The generally smaller reflection coefficient of the p polarization is also the basis of polarized sunglasses; by blocking the s (horizontal) polarization, most of the glare due to reflection from a wet street, for instance, is removed.[18]:348–350
In the important special case of reflection at normal incidence (not involving anisotropic materials) there is no particular s or ppolarization. Both the x and y polarization components are reflected identically, and therefore the polarization of the reflected wave is identical to that of the incident wave. However, in the case of circular (or elliptical) polarization, the handedness of the polarization state is thereby reversed, since byconvention this is specified relative to the direction of propagation. The circular rotation of the electric field around the x-y axes called "right-handed" for a wave in the +z direction is "left-handed" for a wave in the -z direction. But in the general case of reflection at a nonzero angle of incidence, no such generalization can be made. For instance, right-circularly polarized light reflected from a dielectric surface at a grazing angle, will still be right-handed (but elliptically) polarized. Linear polarized light reflected from a metal at non-normal incidence will generally become elliptically polarized. These cases are handled using Jones vectors acted upon by the different Fresnel coefficients for the s and ppolarization components.
Measurement techniques involving polarization
Some optical measurement techniques are based on polarization. In many other optical techniques polarization is crucial or at least must be taken into account and controlled; such examples are too numerous to mention.
Measurement of stress
In engineering, the phenomenon of stress induced birefringence allows for stresses in transparent materials to be readily observed. As noted above and seen in the accompanying photograph, the chromaticity of birefringence typically creates colored patterns when viewed in between two polarizers. As external forces are applied, internal stress induced in the material is thereby observed. Additionally, birefringence is frequently observed due to stresses "frozen in" at the time of manufacture. This is famously observed in cellophane tape whose birefringence is due to the stretching of the material during the manufacturing process.
Ellipsometry
Ellipsometry is a powerful technique for the measurement of the optical properties of a uniform surface. It involves measuring the polarization state of light following specular reflection from such a surface. This is typically done as a function of incidence angle or wavelength (or both). Since ellipsometry relies on reflection, it is not required for the sample to be transparent to light or for its back side to be accessible.
Ellipsometry can be used to model the (complex) refractive index of a surface of a bulk material. It is also very useful in determining parameters of one or more thin film layers deposited on a substrate. Due to their reflection properties, not only are the predicted magnitude of the p and spolarization components, but their relative phase shifts upon reflection, compared to measurements using an ellipsometer. A normal ellipsometer does not measure the actual reflection coefficient (which requires careful photometric calibration of the illuminating beam) but the ratio of the p and sreflections, as well as change of polarization ellipticity (hence the name) induced upon reflection by the surface being studied. In addition to use in science and research, ellipsometers are used in situ to control production processes for instance.[20]:585ff[21]:632
Geology
Photomicrograph of a volcanic sand grain; upper picture is plane-polarized light, bottom picture is cross-polarized light, scale box at left-center is 0.25 millimeter.
The property of (linear) birefringence is widespread in crystalline minerals, and indeed was pivotal in the initial discovery of polarization. In mineralogy, this property is frequently exploited using polarizationmicroscopes, for the purpose of identifying minerals. See optical mineralogy for more details.[22]:163–164
Sound waves in solid materials exhibit polarization. Differential propagation of the three polarizations through the earth is a crucial in the field of seismology. Horizontally and vertically polarized seismic waves (shear waves)are termed SH and SV, while waves with longitudinal polarization (compressional waves) are termed P-waves.[23]:48–50[24]:56–57
Chemistry
We have seen (above) that the birefringence of a type of crystal is useful in identifying it, and thus detection of linear birefringence is especially useful in geology and mineralogy. Linearly polarized light generally has its polarization state altered upon transmission through such a crystal, making it stand out when viewed in between two crossed polarizers, as seen in the photograph, above. Likewise, in chemistry, rotation of polarization axes in a liquid solution can be a useful measurement. In a liquid, linear birefringence is impossible, however there may be circular birefringence when a chiral molecule is in solution. When the right and left handedenantiomers of such a molecule are present in equal numbers (a so-called racemicmixture) then their effects cancel out. However, when there is only one (or a preponderance of one), as is more often the case for organic molecules, a net circular birefringence (or optical activity) is observed, revealing the magnitude of that imbalance (or the concentration of the molecule itself, when it can be assumed that only one enantiomer is present). This is measured using apolarimeter in which polarized light is passed through a tube of the liquid, at the end of which is another polarizer which is rotated in order to null the transmission of light through it.[18]:360–365[25]:169–172
Astronomy
In many areas of astronomy, the study of polarized electromagnetic radiation fromouter space is of great importance. Although not usually a factor in the thermal radiation ofstars, polarization is also present in radiation from coherent astronomical sources (e.g. hydroxyl or methanol masers), and incoherent sources such as the large radio lobes in active galaxies, and pulsar radio radiation (which may, it is speculated, sometimes be coherent), and is also imposed upon starlight by scattering from interstellar dust. Apart from providing information on sources of radiation and scattering, polarization also probes the interstellar magnetic field viaFaraday rotation.[26]:119,124[27]:336–337 The polarization of the cosmic microwave background is being used to study the physics of the very early universe.[28][29] Synchrotron radiation is inherently polarised. It has been suggested that astronomical sources caused the chirality of biological molecules on Earth.[30]











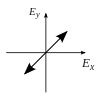
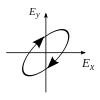








Comments
Post a Comment